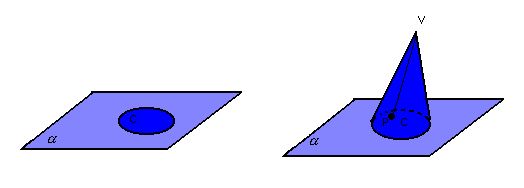
Dado um círculo C, contido num plano
, e um ponto V ( vértice) fora de , chamamos de cone circular o conjunto de todos os segmentos 
.
Elementos do cone circular
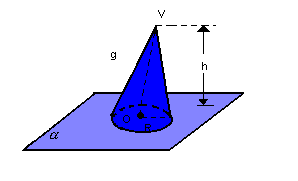
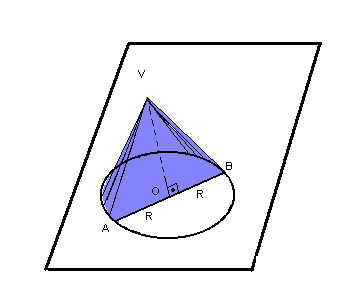
Dado o cone a seguir, consideramos os seguintes elementos:
- altura: distância h do vértice V ao plano
- geratriz (g):segmento com uma extremidade no ponto V e outra num ponto da circunferência
- raio da base: raio R do círculo
- eixo de rotação:reta
determinada pelo centro do círculo e pelo vértice do cone
Cone reto
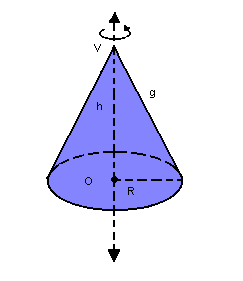
Todo cone cujo eixo de rotação é perpendicular à base é chamado cone reto, também denominado
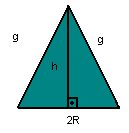
cone de revolução. Ele pode ser gerado pela rotação completa de um triângulo retângulo em torno de um de seus catetos.
Da figura, e pelo Teorema de Pitágoras, temos a seguinte relação:
| g2 = h2 + R2 |
Secção meridiana
A secção determinada, num cone de revolução, por um plano que contém o eixo de rotação é chamada secção meridiana.
Se o triângulo AVB for equilátero, o cone também será equilátero:
Áreas
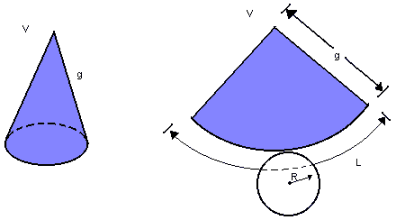
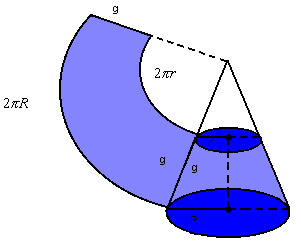
Desenvolvendo a superfície lateral de um cone circular reto, obtemos um setor circular de raio g e comprimento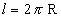 
:
:
Assim, temos de considerar as seguintes áreas:
a) área lateral (AL): área do setor circular
b) área da base (AB):área do circulo do raio R
c) área total (AT):soma da área lateral com a área da base
Volume
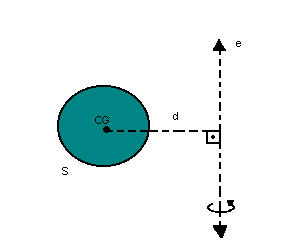
Para determinar o volume do cone, vamos ver como calcular volumes de sólidos de revolução. Observe a figura:
d = distância do centro de gravidade (CG) da sua superfície ao eixo e
S=área da superfície
Sabemos, pelo Teorema de Pappus - Guldin, que, quando uma superfície gira em torno de um eixo e, gera um volume tal que:
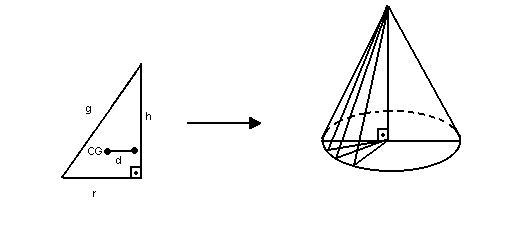
Vamos, então, determinar o volume do cone de revolução gerado pela rotação de um triângulo retângulo em torno do cateto h:
O CG do triângulo está a uma distância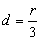 
do eixo de rotação. Logo:
do eixo de rotação. Logo:
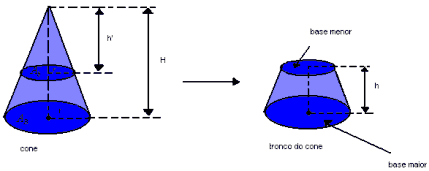
Tronco do cone
Sendo o tronco do cone circular regular a seguir, temos:
- as bases maior e menor são paralelas;
- a altura do tronco é dada pela distância entre os planos que contém as bases.
Áreas
Temos:
a) área lateral
b) área total
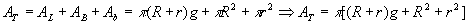
Volume
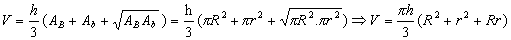
Sendo V o volume do cone e V' o volume do cone obtido pela secção são válidas as relações:
ESFERA
Chamamos de esfera de centro O e raio R o conjunto de pontos do espaço cuja distância ao centro é menor ou igual ao raio R.
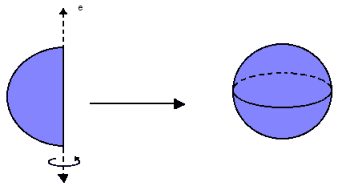
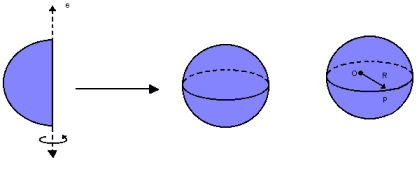
Considerando a rotação completa de um semicírculo em torno de um eixo e, a esfera é o sólido gerado por essa rotação. Assim, ela é limitada por uma superfície esférica e formada por todos os pontos pertencentes a essa superfície e ao seu interior.
Volume
O volume da esfera de raio R é dado por:
 |
Partes da esfera
Superfície esférica
A superfície esférica de centro O e raio R é o conjunto de pontos do es[aço cuja distância ao ponto O é igual ao raio R.
Se considerarmos a rotação completa de uma semicircunferência em torno de seu diâmetro, a superfície esférica é o resultado dessa rotação.
A área da superfície esférica é dada por:
 |
Zona esférica
É a parte da esfera gerada do seguinte modo:
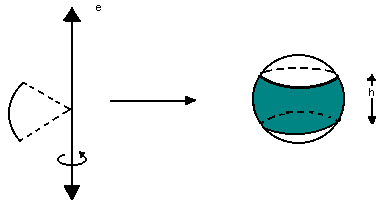
A área da zona esférica é dada por:
 |
Calota esférica
É a parte da esfera gerada do seguinte modo:
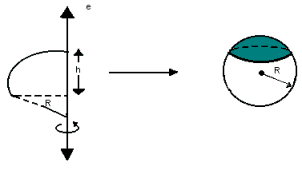
A área da calota esférica é dada por:
|
Fuso esférico
O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semi-circunferência de um ângulo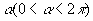 
em torno de seu eixo:
em torno de seu eixo:
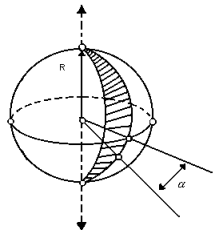
A área do fuso esférico pode ser obtida por uma regra de três simples:
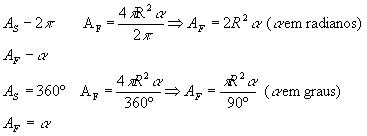
Cunha esférica
Parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo :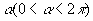
:
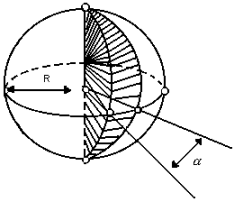
O volume da cunha pode ser obtido por uma regra de três simples:
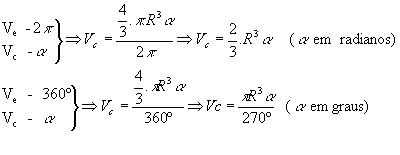
FONTE: http://www.somatematica.com.br/emedio/espacial/espacial24.php
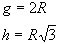
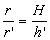
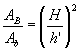
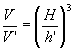
Nenhum comentário:
Postar um comentário